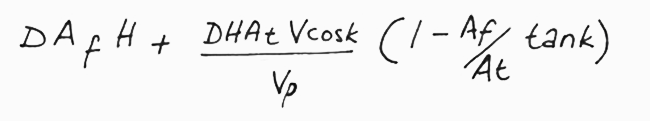When it’s raining what’s the best way to keep dry – Run or Walk ?
When it then starts raining and you don’t have your umbrella with you the age old question is whether you should run or walk. If you run, think of all those extra raindrops that you are colliding with which you would otherwise have missed. On the other hand, if you walk you will be out in the rain for longer, catching lots of rain on your shoulders. Some serious mathematical thought has gone into this question over the years.
One Answer
In a Nutshell : The conclusion has been that, to stay as dry as possible, you should run as fast as you can. Common sense probably told you the same thing.
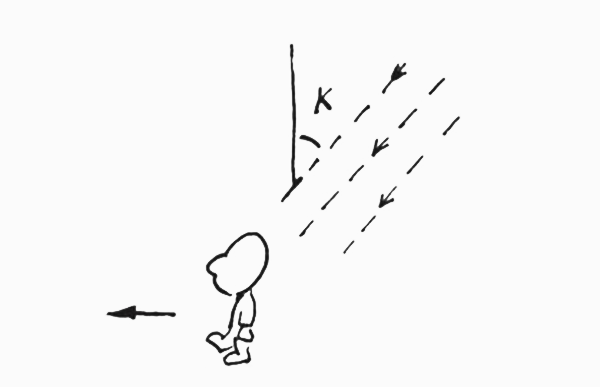
However, (There’s ALWAYS one of those aren’t there!) there is a surprising twist to this problem. The standard solution assumes that the rain is falling vertically. What happens if there is wind and the rain is falling at an angle?
When rain falls vertically and you are standing still, the drops only hit your head and shoulders. If there is wind coming from behind you, however, then some of the rain will also hit your back even when you are standing still. The rain has a horizontal speed as well as a vertical downward speed (hence it’s slant). The surprising twist is that when the rain is coming from behind you, it is sometimes better to walk than run. However, this only applies if you are able to move faster than the horizontal speed of the rain.
Let’s do (some) Maths
Why it is sometimes drier to walk in the rain than run?
 To simplify the calculation, let’s assume that the pedestrian is a rectangular block of wood.
To simplify the calculation, let’s assume that the pedestrian is a rectangular block of wood.
There are seven factors that we have taken into account:
V is the speed at which the rain is falling K is the angle at which the rain is falling D is the density of the rain (in kg per cubic meter) At is the area of the pedestrian’s top Af is the area of the pedestrian’s front H is the distance to the pedestrian’s destination Vp is the speed at which the pedestrian runs
There isn’t space to put in all the algebra, but the way we produced the formula below was to work out separately how much rain hits the front and the top of the pedestrian and then added these two together. The total rain in kilograms falling on the pedestrian as long as he is travelling at least as fast as the horizontal speed of the rain is:
The important part of the formula is the bit in the brackets. If Af /AtTan K comes to more than 1.0 then the right hand part of the formula becomes negative, i.e. the rain hitting the pedestrian is reduced. The pedestrian can control his speed Vpf /AtTan K is greater than 1. (Take a deep breath!)
The ratio of a person’s front area to their top is usually about 5.0. Since the tangent of 15° is about 0.2, this means that if rain is falling at an angle of more than 15°, the driest way to get home without an umbrella is to move at the same speed as the horizontal speed of the rain.
To Sum Up
However, to sum up, the conclusion is this:
If the rain is falling vertically then you should run as fast as you can.
If you are a person of typical build and the rain is coming from behind you at the speed of a gentle walking pace, you will be hit by less rain if you amble along than if you run full pelt.
In other words, there are circumstances when it is better to walk than run! The reason for this apparently odd outcome is that under the conditions described, if you run faster, the additional rain hitting your front is greater than the loss of rain hitting your head by taking less time to make it home.
Of course by the time you’ve worked all this out you will be wetter than if you had not known about the formula at all!