Philosophy is full of perplexing paradoxical thought experiments and Zeno’s paradox is, as the Americans would, say a doozy – although Zeno was actually a 5th Century B.C. Greek philosopher so I’m sure he wouldn’t have described it a such.

ZENO’S THOUGHT EXPERIMENT…

This is about a race between the fleet-footed hero of the Trojan War, Achilles and a tortoise : Naturally, Achilles can run faster than the tortoise, so the tortoise is given a big head start. The race starts —Achilles’s first goal is to get to the point where the tortoise started. Of course, by then the tortoise has moved a little way. So now Achilles has to get to that spot. By the time he gets there, the tortoise has moved again. No matter how many times Achilles reaches the tortoise’s prior location, even if he does it an infinite number of times, Achilles will never catch up with the tortoise, although he’ll get awfully close. All the tortoise needs to do to win the race is not to stop. This is essentially another way of describing Zeno’s racetrack paradox : In order to get to the end of the racetrack, a runner must first complete an infinite number of journeys. He must run to the midpoint; then he must run to the midpoint of the remaining distance; then to the midpoint of the still remaining distance, etc., etc. Theoretically speaking, because he has to get to midpoints an infinite number of times, he can never get to the end of the track. But of course we know that Achilles WILL overtake the tortoise and that the runner WILL get to the end of the track.

Achilles’ task seems impossible because he “would have to do an infinite number of ‘things’ in a finite amount of time

The logic of the thought experiment seems to hold up but we know from experience that it can’t be true so what’s going on ?

The problem has to do with our conception of infinity and there’s more than one kind of infinity.

Convergent Series

There are divergent series and convergent series. The most obvious divergent series is 1 + 2 + 3 + 4 … There’s no answer to that equation. Or, more precisely, the answer is “infinity.” If Achilles had to cover these sorts of distances over the course of the race—in other words, if the tortoise were making progressively larger gaps rather than smaller ones—Achilles would never catch the tortoise.

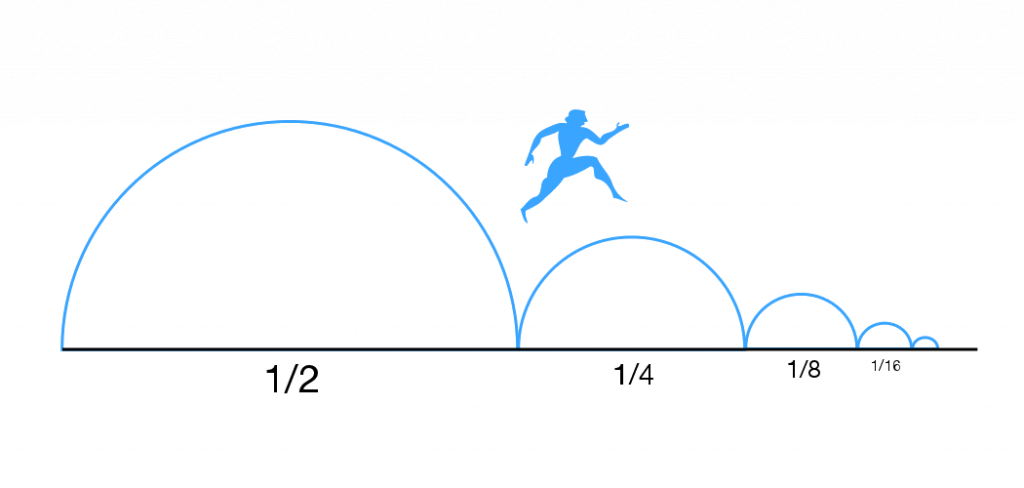
Now consider the series ¹/₂ + ¹/₄ + ¹/₈ + ¹/₁₆ … Although the numbers go on forever, the series converges, and the solution is 1. As long as Achilles is making the gaps smaller at a sufficiently fast rate, so that their distances look more or less like this equation, he will complete the series in a measurable amount of time and catch the tortoise.

The convergence of infinite series explains countless things we observe in the world. Not just the fact that a fast runner can overtake a tortoise in a race, either. Any distance, time, or force that exists in the world can be broken into an infinite number of pieces—just like the distance that Achilles has to cover—but centuries of physics and engineering work have proved that they can be treated as finite.

That answer might not fully satisfy ancient Greek philosophers, many of whom felt that their logic was more powerful than observed reality. But the way mathematicians and philosophers have answered Zeno’s challenge, using observation to reverse-engineer a durable theory, is a testament to the role that research and experimentation play in advancing understanding.